Atomsk
Le couteau suisse pour les simulations atomiques

Le couteau suisse pour les simulations atomiques

Ce tutoriel explique comment utiliser Atomsk pour construire des systèmes avec n'importe quelle orientation cristallographique, en utilisant le mode "--create", et/ou les options "-rotate", "-orthogonal-cell", et "-reduce-cell". Il est recommandé d'être familier avec la cristallographie et les indices de Miller pour suivre ce tutoriel.
▶ Pour plus d'informations, référez-vous à la page de documentation correspondante.
L'orientation cristalline peut être un concept épineux, car il nécessite de bien se représenter le cristal dans l'espace en 3 dimensions, ses directions et plans cristallographiques, ce qui peut être source de confusion pour les étudiants et les débutants. Pour cette raison, nous allons d'abord définir certains concepts clés. Dans une simulation, trois jeux de vecteurs peuvent être distingués, et ne doivent pas être confondus les uns avec les autres :
Quand on considère une maille élémentaire d'un matériau cubique, ces trois jeux de vecteurs sont souvent confondus : la direction [100] du cristal est alignée avec la direction cartésienne X, et les vecteurs de boîte sont exactement les mêmes que les vecteurs du réseau. C'est souvent la représentation qui est faite dans les livres de cristallographie, et elle peut mener à une confusion chez les débutants -par exemple, comme je l'ai lu parfois, croire que [100] est "la direction X du cristal", ce qui ne peut que mener à des erreurs.
Il est impératif de différencier ces vecteurs et directions. D'abord, les axes cartésiens X, Y, Z, sont définis par convention, c'est-à-dire qu'ils sont choisis arbitrairement au début du problème, et ne changent plus par la suite. Ils représentent la métrique rigide et indéformable de l'espace, au sens de l'espace absolu de Newton : indépendants du temps, et indépendants de tout ce qu'il peut se passer dans cet espace, comme l'ajout d'atomes, la rotation d'un cristal ou n'importe quoi d'autre.
Ensuite, à l'intérieur de cet espace cartésien, les axes du cristal pointent dans des directions qui sont définies par la cristallographie. Il est possible de tourner le cristal, ce qui fera tourner les axes cristallographiques par rapport aux directions cartésiennes (fixes). Un cristal peut avoir son axe [100] aligné avec l'axe cartésien X, mais rien n'oblige à ce que ce soit toujours le cas. Par exemple, on peut tourner le cristal de sorte que son axe [110] soit aligné avec X. Ou, on peut vouloir que l'axe [111] du cristal soit aligné avec Z. Par raccourci, l'orientation du cristal par rapport aux axes cartésiens est souvent notée avec un signe "égal", par exemple "X=[110]" ou "Z=[111]".
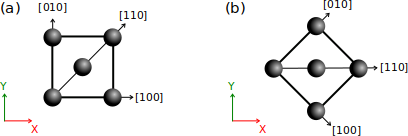
(a) Par défaut, une maille d'un cristal parfait (par ex. cfc) est créé avec son axe cristallin [100] aligné avec l'axe cartésien X, [010] aligné avec Y, et [001] suivant Z (ce dernier n'est pas représenté, il pointerait perpendiculairement à la figure).
(b) Si le cristal est tourné de 45°, alors c'est l'axe cristallin [110] qui devient aligné avec X. Notez que le repère cartésien (X,Y,Z) est défini par convention et ne change pas.
Enfin, les vecteurs de boîte peuvent aussi tourner, ou être changés suivant ce que l'on souhaite faire. Un exemple simple, si vous démarrez d'une maille élémentaire et la dupliquez pour former une super-cellule, alors les directions cristallines restent les mêmes, mais les vecteurs de boîte changent. Parfois, on s'attend ou on veut que les vecteurs de boîte soient alignés avec les axes cartésiens. Cependant dans le cas le plus général ce n'est pas forcément le cas, et les vecteurs de boîte peuvent avoir n'importe quelles composantes suivant X, Y et Z (lisez le tutoriel précédent sur les conditions aux limites). Si on souhaite maintenir la périodicité du cristal (les fameuses "conditions aux limites périodiques"), alors les vecteurs de boîte doivent être des combinaisons linéaires des vecteurs du réseau cristallin. Mais là encore, dans le cas général ce n'est pas toujours le cas, parfois il n'est même pas possible de maintenir la périodicité (par exemple lorsque le cristal contient des défauts étendus comme des dislocations).
En résumé, quand on parle d'orientation cristalline, il faut avoir les idées claires des différents vecteurs entrant en jeu, et ne pas les confondre. Dans la suite, vous allez apprendre comment orienter un cristal par rapport aux axes cartésiens avec Atomsk.
Dans un tutoriel précédent, vous avez appris comment générer des mailles simples avec Atomsk. Maintenant nous allons voir comment choisir une orientation cristalline différente. Pour cela, après les paramètres du mode "--creat", ajoutez le mot-clé "orient" et les trois directions cristallines (en notation de Miller) que vous souhaitez suivant X, Y, et Z.
Par exemple, pour créer une maille de cuivre cfc avec la direction [110] suivant X, [110] suivant Y, et [001] suivant Z, exécutez la commande suivante :
atomsk --create fcc 3.597 Cu orient [110] [-110] [001] Cu.cfg
ⓘ Les indices de Miller doivent être entrés sous la forme d'une chaîne de caractères continue (pas d'espace entre les indices). Les crochets [] sont optionnels et peuvent être omis, par exemple "orient 110 -110 001". Les indices de Miller supérieurs ou égaux à 10 doivent être séparés par une barre de soulignement, par exemple : "10_-12_0".
Une chose importante à retenir, est que les vecteurs donnés doivent suivre la notation de Miller, et doivent former une base orthogonale. Si les vecteurs ne sont pas perpendiculaires entre eux, alors Atomsk affichera un message d'erreur et abandonnera. Vous pouvez visualiser le système final ("Cu.cfg") avec OVITO :
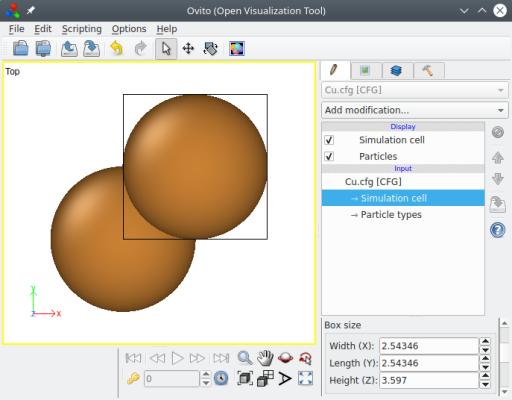
Atomsk a automatiquement utilisé les directions cristallines données comme vecteurs de boîte, de sorte que la boîte finale est orthogonale. Lorsque c'est possible, Atomsk tient compte des symétries du cristal pour réduire la taille de boîte, afin de produire la maille élémentaire la plus petite possible. Dans le réseau cfc, le plus petit vecteur le long d'une direction [hkl], est en fait ½[hkl] si l'un des indices de Miller est impair et les deux autres pairs. Dans l'exemple ci-dessus, on s'attendrait à ce que la boîte ait une longueur de 3.597√2 = 5.087 Å le long de la direction [110]. Au lieu de cela, Atomsk l'a réduite de moitié. Le but est de fournir la plus petite maille qui respecte l'orientation cristalline demandée. Dans cette orientation, la maille compte deux atomes, comme vous pouvez le voir dans OVITO.
Atomsk supporte cette méthode pour tous les réseaux cubiques, et pour toutes les directions cristallines. Par exemple, créons une maille orientée de fer telle que X=[121], Y=[101], et Z=[111] :
atomsk --create bcc 2.85 Fe orient [121] [-101] [1-11] Fe.xsf
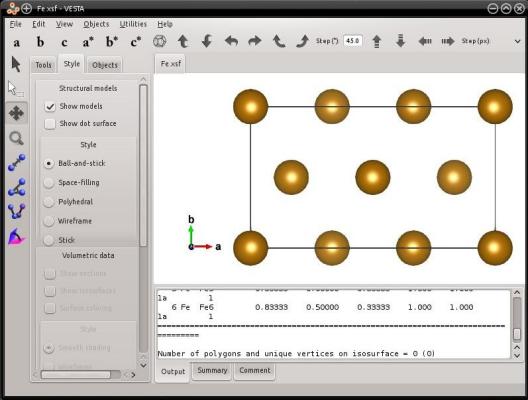
Comme précédemment, Atomsk exploite les symétries du réseau pour réduire la taille de boîte. Dans le réseau cubique centré, la période suivant une direction [hkl] est réduite à ½[hkl] lorsque les trois indices de Miller sont impairs. Dans cet exemple, c'est le cas pour la direction [111]. Dans cette orientation la maille compte 6 atomes.
Le mode "--create" permet de générer de nombreuses mailles cubiques (comme le diamant, zincblende, perovskite...). À titre d'exercice, vous pouvez vous entraîner à les générer, et à choisir différentes orientations cristallines.
Atomsk peut aussi orienter des mailles hexagonales au moment de leur création : hexagonal compact (hcp), wurtzite, et graphite. Cependant, "orientation cristalline" prend un sens légèrement différent par rapport aux mailles cubiques.
Pour l'exemple, créons une maille élémentaire de magnésium hcp. Lorsqu'on génère une maille hcp avec le mode "--create", les vecteurs de boîte suivent le réseau hexagonal, et donc l'un des vecteurs de boîte (le second ici) n'est pas aligné avec un axe cartésien :
atomsk --create hcp 3.21 5.213 Mg Mg.xsf
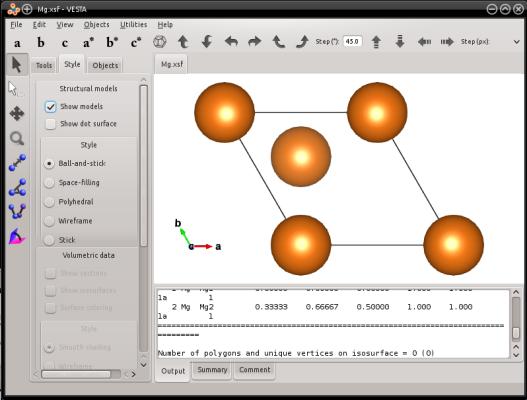
Comme vous devez le savoir, dans un réseau hexagonal les directions cristallines sont repérées avec quatre indices de Miller [hkil], qui doivent satisfaire h+k+i=0 (si vous n'êtes pas familier avec cette notation, référez-vous à un livre de cristallographie). Avec une maille hexagonale, vous pouvez utiliser le mot-clé "orient" suivi par trois vecteurs [hkil]. Atomsk utilisera ces vecteurs pour construire la boîte, et la remplira d'atomes. Ensuite, le premier vecteur de boîte sera aligné avec l'axe cartésien X, le second vecteur de boîte sera placé dans le plan XY, et le troisième pointera hors du plan XY.
Construisons une maille orientée de magésium hcp :
atomsk --create hcp 3.21 5.213 Mg orient [0-110] [0001] [2-1-10] xsf
Ces trois vecteurs se trouvent être orthogonaux, de sorte que la direction cristalline [0110] sera alignée avec l'axe cartésien X, [0001] avec Y, et [2110] avec Z. La maille ressemblera à cela :
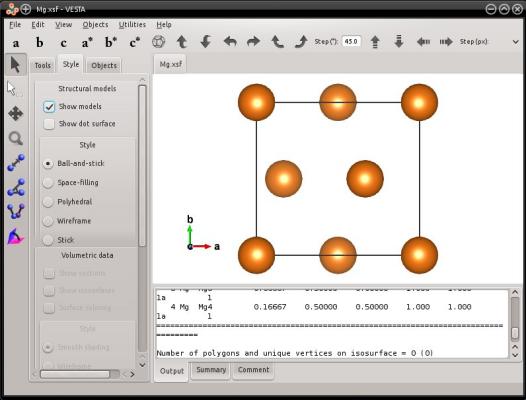
Cela dit, dans le cas des mailles hexagonales, les vecteurs de Miller n'ont pas forcément à être orthogonalxu. Il est possible de fournir n'importe quelle direction cristalline, et Atomsk construira une boîte avec les vecteurs demandés. Cela peut être illustré par l'exemple suivant :
atomsk --create hcp 3.21 5.213 Mg orient [0-110] [10-10] [0001] xsf
Dans cet exemple, les directions hexagonales [0110] et [1010] ne sont pas orthogonales. Atomsk va donc créer une boîte où le premier vecteur H1 sera [0110] et aligné avec l'axe cartésien X ; le second vecteur de boîte H2=[1010] sera dans le plan XY (notez qu'il N'EST PAS aligné avec l'axe Y) ; et le troisième vecteur de boîte H3=[0001] pointera en-dehos du plan XY (dans cet exemple particulier, [0001] est aligné avec Z, mais on aurait pu choisir un vecteur différent). Au final, le système ressemblera à cela :
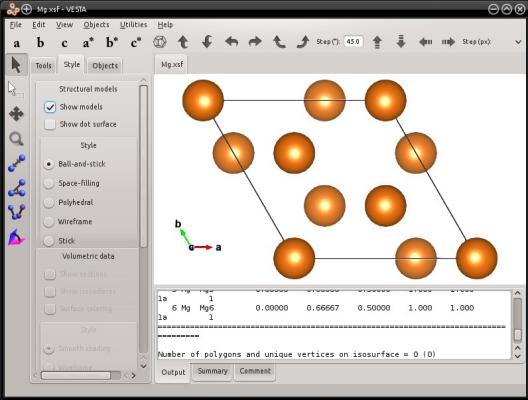
De cette façon, il est possible de créer des mailles hexagonales où l'axe de symétrie 3 est toujours visible. Vous pouvez essayer des commandes similaires avec d'autres mailles hexagonales, comme wurtzite ou graphite.
Il est important de garder en tête que, contrairement aux réseaux cubiques, les systèmes hexagonaux orientés ne produisent pas forcément des boîte orthogonales. Dans le cas des réseaux hexagonaux, les directions cristallines que vous fournissez ne deviennent pas forcément alignées avec les axes cartésiens elles servent à définir les vecteurs de boîte. Si vous souhaitez obtenir une boîte orthogonale équivalente, vous pouvez utiliser l'option "-orthogonal-cell", comme expliqué dans la section 4 ci-dessous.
De la façon la plus générale, une rotation est une transformation qui modifie les directions cristallines qui se trouvent suivant les axes cartésiens X, Y et Z. Pour l'illustrer, nous pouvons utiliser l'option "-rotate" pour tourner un cristal :
atomsk initial.xsf -rotate Z 33 final.xsf
Dans ce cas, selon l'axe de rotation et l'angle choisis, des directions cristallines différentes peuvent se retrouver suivant les trois axes cartésiens. Pour le contrôler, cela nécessite de savoir exactement comment tourner le cristal.
Pour cette raison, l'option "-rotate" peut être assez lourde à utiliser, surtout si on veut obtenir une orientation cristalline non triviale. Pour des orientations plus complexes, il peut être plus pratique d'utiliser l'option "-orient" (à ne pas confondre avec le mot-clé "orient" qui appartient au mode "--create", comme expliqué précédemment). Pour l'exemple, supposons que nous partions d'une maille (non orientée) de fer, générée de la façon suivante :
atomsk --create bcc 2.85 Fe Fe.xsf
Vous pouvez utiliser l'option "-orient" pour la tourner vers une autre orientation. Cette option requiert l'orientation cristalline de départ (3 vecteurs en notation de Miller), suivie de l'orientation cristalline à laquelle on souhaite arriver (3 autres vecteurs, toujours en notation de Miller). Ici, l'orientation de départ est simplement [100] suivant X, [010] suivant Y, et [001] suivant Z. Opérons une rotation afin que la direction [121] soit suivant X, [101] suivant Y, et [111] suivant Z :
atomsk Fe.xsf -orient [100] [010] [001] [121] [-101] [1-11] Fe_orient.cfg
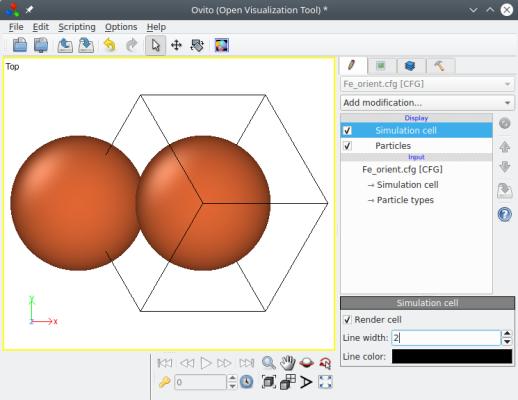
Lorsque vous ouvrez ce fichier pour le visualiser dans OVITO, remarquez le repère cartésien (x,y,z) affiché en bas à gauche. Comme vous pouvez le voir, l'option "-orient" applique une rotation rigide du système, boîte et atomes, par rapport au repère (fixe) cartésien. Résultat, les vecteurs de boîte ne sont plus alignés avec les axes cartésiens chaque vecteur de boîte a des composantes suivants X, Y et Z.
C'est là un autre point fondamental à garder en tête : si vous appliquez une rotation, cela ne veut pas dire que Atomsk va "magiquement" re-créer une boîte orthogonale. Chaque vecteur de boîte peut tourner, et avoir des composantes (x,y,z). Atomsk peut très bien travailler avec des vecteurs de boîte arbitraires. Notez que cela n'est pas forcément vrai de tous les codes de simulation ou de visualisation, certains ont des limitations sur les vecteurs de boîte qu'ils peuvent supporter.
Si vous souhaitez conserver une orientation cristalline donnée, et obtenir une boite orthogonale équivalente, alors poursuivez avec la section 4 ci-dessous.
Pour obtenir une boîte orthogonale à partir de n'importe quel système, une autre méthode est disponible dans Atomsk l'option "-orthogonal-cell". Cette option peut travailler depuis n'importe quels vecteurs de boîte initiaux (même s'ils ne sont pas orthogonaux entre eux, ou s'ils ne sont pas alignés avec les axes cartésiens). Puis, elle essaye de trouver les meilleures combinaisons linéaires de ces vecteurs initiaux, qui produisent de nouveaux vecteurs alignés avec les axes cartésiens X, Y, et Z. Ces nouveaux vecteurs définissent alors une nouvelle boîte, qui est orthogonale. Ensuite, les atomes sont dupliqués pour remplir cette nouvelle boîte. À la fin, on obtient une boîte orthogonale qui a la même orientation cristalline que le système de départ, et qui respecte la périodicité du cristal.
Cette option peut être utilisée après avoir tourné un cristal de n'importe quel angle. Pour illustrer comment ça marche, décomposons les étapes pas à pas. D'abord, créons une maille de cuivre cfc, et tournons-la de 45° autour de l'axe Z :
atomsk --create fcc 3.597 Cu -rotate Z -45 Cu_rotated.cfg
La visualisation nous montre que tout le système (boîte+atomes) a effectivement été tourné, comme expliqué dans la section 3 ci-dessus :
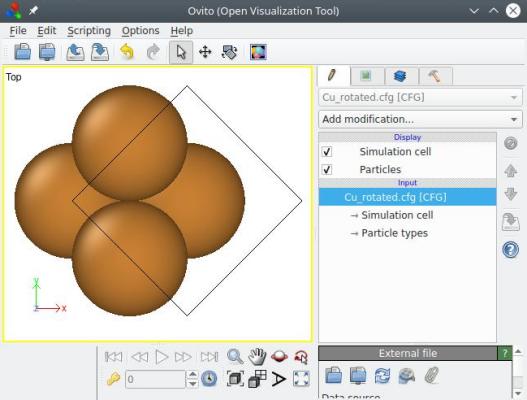
Maintenant, la direction [110] se trouve suivant X, et [110] suivant Y (la direction [001] étant l'axe de rotation, elle est toujours suivant Z). Cependant, les vecteurs de boîte eux, ne sont plus alignés avec les directions cartésiennes. Pour rétablir cela, utilisons l'option "-orthogonal-cell" (cette option ne demande aucun paramètre) :
atomsk Cu_rotated.cfg -orthogonal-cell Cu_ortho.cfg
Après avoir appliqué cette option, l'orientation cristalline est préservée (c'est-à-dire que la direction [110] est toujours suivant X, et ainsi de suite), mais maintenant les trois vecteurs de boîte sont aussi alignés avec X, Y et Z respectivement. De plus, les atomes ont été dupliqués pour remplir cette nouvelle boîte, de sorte que le nombre d'atomes dans le système a changé :
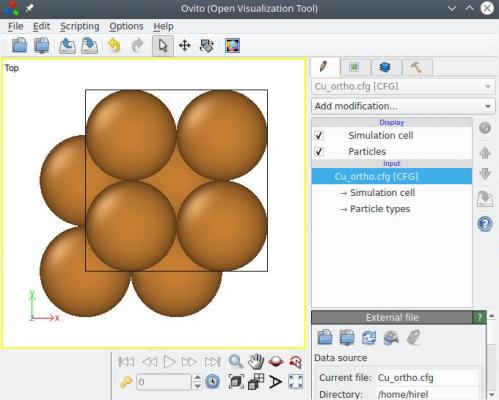
Contrairement à la méthode expliquée dans la section 1 ci-dessus, l'option "-orthogonal-cell" n'utilise pas les symétries du cristal pour tenter de réduire la boîte. Ainsi, cette fois la boite finale prend la taille d'un vecteur <110> entier suivant X et Y, c'est-à-dire 3.597√2 (et non la moitié). C'est parce que l'option "-orthogonal-cell" ignore complètement le type de réseau cristallin, elle n'a donc aucune connaissance des symétries qui pourraient être utilisées. Si vous souhaitez réduire la taille de boîte, vous pouvez utiliser l'option "-reduce-cell" après celle-ci (voir la section suivante).
Au passage, toutes les étapes précédentes peuvent être réalisées en une seule commande :
atomsk --create fcc 3.597 Cu -rotate Z -45 -orthogonal-cell Cu_ortho.cfg
Bien entendu, pour les réseaux cubiques cette méthode est assez lourde, et la méthode utilisant le mode "--create" est mieux adaptée. L'intérêt de l'option "-orthogonal-cell" est qu'elle peut être utilisée avec n'importe quel type de système, ce qui la rend très puissante et utile pour les réseaux non-cubiques.
Comme expliqué dans la section précédente, l'option "-orthogonal-cell" ne connaît pas les symétries en vigueur dand le cristal. En conséquence, la boîte obtenue ("Cu_ortho.cfg") a la bonne orientation, mais ce n'est pas la plus petite boîte possible correspondant à cette orientation. Rien qu'en la regardant dans OVITO, on peut deviner qu'il est possible de la réduire de moitié suivant X et Y.
Atomsk propose une option "-reduce-cell", qui tente de réduire la taille d'une boîte tout en préservant la périodicité du cristal. Pour cela, elle recherche des atomes équivalents suivant chaque vecteur de boîte, et détecte le plus petit vecteur joignant deux atomes équivalents.
atomsk Cu_ortho.cfg -reduce-cell Cu_unitcell.cfg
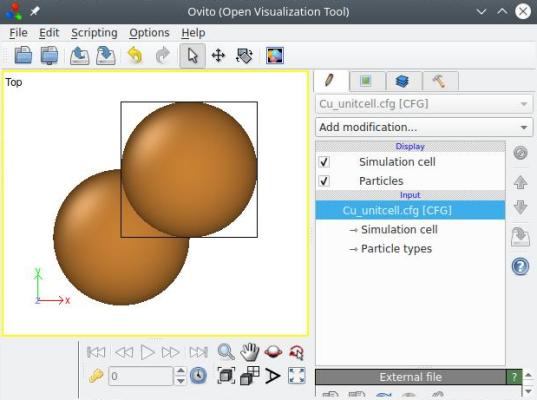
Avec cette option, le système est réduit à deux atomes, ce qui est bien la plus petite boîte possible pour cette orientation cristalline. Encore une fois, toutes les options précédents peuvent être appelées dans une seule et même commande :
atomsk --create fcc 3.597 Cu -rotate Z -45 -orthogonal-cell -reduce-cell Cu_unitcell.cfg
Transformons le réseau hcp de magnésium précédent en boîte orthogonale. Comme dans la section 2 ci-dessus, si nous générons une maille de magnésium hcp, alors le deuxième vecteur de boîte n'est pas aligné avec Y :
atomsk --create hcp 3.21 5.213 Mg Mg.xsf

Si maintenant nous utilisons l'option "-orthogonal-cell" sur ce système, nous obtenons un réseau équivalent dans une boîte orthogonale :
atomsk --create hcp 3.21 5.213 Mg -orthogonal-cell Mg_ortho.xsf
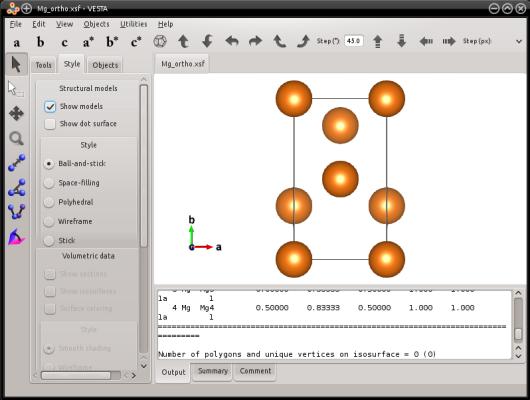
Il s'agit là exactement du même réseau hexagonal, avec la même orientation cristalline. La seule chose qui a changé, c'est que d'autres vecteurs de réseau ont été utilisés, pour obtenir une boîte orthogonale. De cette façon, la périodicité du cristal est préservée. La seule chose différente est que maintenant, les trois vecteurs de boîte sont orthogonaux entre eux. Aussi, des atomes ont été ajoutés dans leurs sites cristallographiques équivalents, afin de remplir la nouvelle boîte.
Cette option peut aussi être utile pour les mailles hexagonales orientées. Comme expliqué dans la section 2 ci-dessus, lors de la création d'une maille hexagonale orientée, la boîte n'est pas nécessairement orthogonale. Mais vous pouvez maintenant la rendre orthogonale, grâce à l'option "-orthogonal-cell". Essayons avec le même exemple que dans la section 2 ci-dessus, simplement en ajoutant l'option "-orthogonal-cell" :
atomsk --create hcp 3.21 5.213 Mg orient [0-110] [10-10] [0001] -orthogonal-cell xsf
Le système final est effectivement contenu dans une boîte orthogonale :
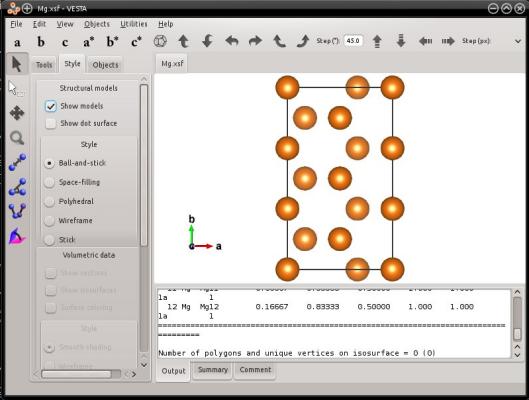
Nous devons écrire un avertissement ici, car la commande ci-dessus et la visualisation peuvent être difficiles à interpréter. Dans cet exemple, la direction [1010] N'EST PAS alignée avec l'axe Y! Comme expliqué en section 2, cette direction cristalline a été utilisée pour générer la boîte de départ (voir la même commande sans l'option "-orthogonal-cell", dans la section 2 ci-dessus). Après avoir exécuté l'option "-orthogonal-cell", les vecteurs de boîte sont changés, de sorte que la direction cristalline [1010] ne correspond plus à un vecteur de boîte, et n'est pas alignée avec un axe cartésien non plus. Si vous voulez savoir quelle direction cristalline est alignée avec quel axe cartésien, alors vous devrez le déterminer vous-même en utilisant la cristallographie. En résumé, soyez très prudent lorsque vous utilisez l'option "-orthogonal-cell", et une fois encore, ne mélangez pas les axes cartésiens, les vecteurs de boîte, et les directions cristallines.
De façon optionnelle, vous pouvez là aussi utiliser l'option "-reduce-cell" pour obtenir une plus petite boîte :
atomsk --create hcp 3.21 5.213 Mg orient [0-110] [10-10] [0001] -orthogonal-cell -reduce-cell Mg_unitcell.xsf
Le système résultant est effectivement plus petit, mais respecte toujours la périodicité du cristal :
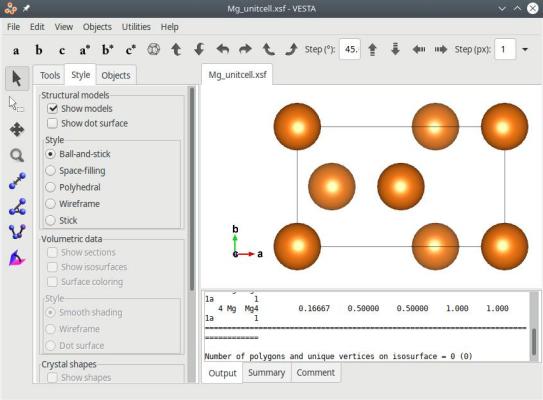
Au lieu des étapes ci-dessus, vous pouvez aussi tourner le système d'un angle arbitraire avec l'option "-rotate", et ensuite utiliser l'option "-orthogonal-cell". Par exemple, nous pouvons facilement déterminer que tourner un cristal hcp de -30° autour de Z aligne l'axe cristallin [1120] avec l'axe cartésien X. Ensuite, nous n'avons plus qu'à utiliser l'option "-orthogonal-cell" pour obtenir une boîte orthogonale équivalente :
atomsk --create hcp 3.21 5.213 Mg -rotate Z -30 -orthogonal-cell Mg_110.xsf
Ainsi, en appliquant les rotations appropriées et en utilisant l'option "-orthogonal-cell", vous pouvez obtenir une boîte orthogonale pour n'importe quelle orientation cristalline que vous souhaitez. Après cela, vous pouvez dupliquer cette boîte (avec l'option "-duplicate") pour obtenir une super-cellule, et poursuivre la construction de votre système atomique.
Après avoir appliqué l'option "orthogonal-cell", la boîte finale peut être très large et contenir beaucoup d'atomes (parfois plusieurs milliers). Comme expliqué ci-dessus, c'est parce que Atomsk recherche des combinaisons linéaires des vecteurs de boîte initiaux, et n'a aucune idée si un vecteur plus court pourrait satisfaire la périodicité du système.
Dans certains cas, l'option "-orthogonal-cell" peut échouer totalement à trouver une boîte appropriée. C'est typiquement le cas lorsque les vecteurs de boîte initiaux forment un angle très aigu, ou ont des longueurs incommensurables. Dans de tels cas, il peut être utile de réduire l'inclinaison de la boîte avec l'option "-unskew" avant d'appeler l'option "-orthogonal-cell". Cependant, si Atomsk échoue toujours malgré tout, alors vous devrez peut-être repenser la géométrie de votre système et la façon de le construire.
L'option "-reduce-cell" est conçue pour les cristaux parfaitement régulier, et devrait fonctionner dans une large majorité de cas. Cependant il ne faut pas s'attendre à ce qu'elle fonctionne correctement avec des systèmes contenant des défauts (lacunes, amas, dislocations...), ni pour les systèmes non-cristallins.