• 

  Accueil

• 

  Télé­charge­ment

• 

  Docu­menta­tion

• 

  Tutoriels

• 

  Citations

• 

  Contributeurs

• 

  Contact

• 

  Liens

Tutoriel : Dislocation en Milieu Anisotrope

Ce tutoriel explique comment créer une dislocation dans un milieu anisotrope, en utilisant le fer comme exemple. This tutorial explains how to construct dislocations in an anisotropic medium, using iron as an example. Il est recommandé d'être familier avec la théorie des dislocations afin de suivre ce tutoriel.

▶ Pour plus d'information, référez-vous à la page de documentation correspondante.

Dans des tutoriels précédents, vous avez appris à insérer des dislocations rectilignes à caractère coin et à caractère vis. Ces méthodes utilisent l'élasticité isotrope, pour laquelle les déplacements dus à une dislocation dépendent uniquement du vecteur de Burgers, et pas des constantes élastiques du matériau (pour les dislocations coin, seul le coefficient de Poisson est nécessaire).

Lorsque le matériau est anisotrope, les déplacements dus à une dislocation dévient de ces solutions isotrope, et les constantes élastiques jouent un grand rôle. Avant d'exécuter des simulations dans un tel matériau, il est souvent opportun de construire une configuration de départ qui contient des déplacements appropriés.

Pour les besoins de ce tutoriel, nous allons construire des dislocations dans le fer α à structure cubique centrée (cc), qui est un matériau anisotrope. Il est connu que les dislocations les plus communes dans ce matériau ont un vecteur de Burgers ½⟨111⟩.

1. Orientation cristallographique du système

La première chose à déterminer est le caractère (coin, vis, ou mixte) de la dislocation que vous souhaitez étudier. Ensuite, il faut créer une super-cellule avec une orientation cristallographique qui permette de construire et d'étudier cette dislocation.

Nous commencerons par construire une dislocation vis. Supposons que nous voulions la ligne de dislocation (et donc aussi le vecteur de Burgers) suivant Z, la direction cristallographique sera donc Z=[111]. Les deux autres directions devront être perpendiculaires à Z, choisissons donc X=[121] et Y=[101].

Pour générer une maille avec cette orientation, nous pouvons utiliser :

atomsk --create bcc 2.856 Fe orient [121] [-101] [1-11] xsf

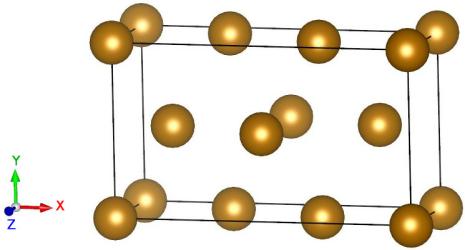
Il est pratique d'avoir ainsi une première visualisation de la cellule de départ orientée.

2. Écrire le tenseur élastique dans un fichier

Puisque nous voulons utiliser l'élasticité anisotrope, il faut fournir le tenseur des constantes élastiques du fer à Atomsk. La première question que vous devez vous poser est : quelles valeurs vais-je fournir ? Vous allez certainement chercher des valeurs dans la littérature, mais vous pouvez trouver plusieurs valeurs différentes, provenant soit de données expérimentales, de calculs ab initio, ou de simulations avec des potentiels inter-atomiques. Laquelle de ces valeurs utiliser ?

La règle d'or est : utilisez des valeurs cohérentes avec le modèle que vous utilisez. Si votre but est d'effectuer des calculs ab initio, alors utilisez des constantes élastiques déterminées avec le même type de méthode, même pseudopotentiel, mêmes approximations, etc. Si vous voulez utiliser un potentiel inter-atomique, utilisez des constantes élastiques déterminées à l'aide de ce potentiel. Ainsi, la dislocation construite sera plus proche de l'état stable, et cela devrait minimiser les contraintes indésirables, surtout si vous utilisez des conditions aux limites fixes (bords figés).

Une fois que vous avez choisi vos valeurs des constantes élastiques, écrivez le tenseur complet dans un fichier texte (les valeurs ci-dessous sont données à titre d'exemple, et les lignes commançant par le symbole # sont des commentaires qui peuvent être supprimés :

De façon alternative, puisque le fer α est orthotrope, il est possible d'utiliser la notation de Voigt. Le fichier texte est alors considérablement raccourci, et ressemble à cela :

Maintenant, le problème est que ce tenseur correspond à un cristal de fer non orienté, c'est-à-dire à l'orientation cristalline X=[100], Y=[010], Z=[001]. Or, ici nous voulons construire un système d'orientation différente, ce qui nécessite d'appliquer une rotation au tenseur des constantes élastiques. Avec Atoms, il suffit de spécifier l'orientation voulue dans le fichier texte, et Atomsk se chargera lui-même d'appliquer la rotation correspondante :

Notez que la section commençant par le mot-clé "orientation" doit apparaître après la section "elastic", pour que la rotation soit bien appliquée au tenseur.

3. Générer un système contenant une dislocation vis

atomsk --create bcc 2.856 Fe orient [121] [-101] [1-11] \
-duplicate 20 30 1 \
-prop elastic.txt \
-disloc 0.501*box 0.501*box screw z y 2.47336855321 \
Fe_dislo.cfg

Cette commande en une seule ligne génère complètement le système contenant la dislocation. Atomsk va d'abord créer une maille de fer avec l'orientation demandée (grâce au mode "--create"), puis la dupliquer pour former une super-cellule, puis lire le fichier contenant le tenseur élastique et lui appliquer la rotation, et enfin introduire la dislocation vis. Puisque nous avons fourni un tenseur élastique, Atomsk utilisera automatiquement les équations de l'élasticité anisotrope pour construire la dislocation.

ⓘ La position de la dislocation peut être donnée comme une fraction des vecteurs de boîte comme ci-dessus ("0.51*box"), ou bien directement en Angströms. La position donnée ne devrait pas correspondre exactement à la position d'un atome, sinon cet atome aurait un déplacement infini. Si vous obtenez des résultats étranges comme des discontinuités, des trous ou de très grands déplacements, alors essayez de changer légèrement la position de la dislocation.

Puisque le vecteur de Burgers est ½[111], sa norme est a√3/2, ce qui donne b=2.47336855321 Å. Notez que la valeur du vecteur de Burgers doit être aussi précise que possible. Atomsk ne fera aucun ajustement, et ne devinera pas la "meilleure valeur" du vecteur de Burgers à votre place.

Atomsk calcule également les contraintes théoriques associées à la dislocation, telles que définies par l'élasticité anisotrope :

       σij = ℜ{ (-2πi)-1 ∑(n=1,3) Bijk(n) Ak(n) D(n) / (x1+P(n)x2) }

Le fichier final "Fe_dislo.cfg" peut être ouvert dans Atomeye ou OVITO. Dans ces logiciels, les composantes des contraintes théoriques σ_xx, σ_yy, σ_zz, etc. peuvent être visualisées. À titre d'exemple, la composante σ_zz devrait ressembler à cela :

De façon similaire à la dislocation vis dans l'aluminium, il est possible de restaurer la périodicité du système le long de la direction de glissement (ici, suivant X) en ajoutant une composante suivant Z égale à b/2 au premier vecteur de la boîte.

4. Introduire une dislocation coin

Au lieu d'une dislocation vis, il est aussi possible d'introduire une dislocation à caractère coin. Il faut alors prêter attention à deux choses. Premièrement, en supposant que nous voulions la ligne de dislocation suivant Z comme précédemment, alors l'orientation du cristal doit être changée : nous utiliserons X=[111], de sorte que le vecteur de Burgers b=[111] soit suivant X et normal à la ligne de dislocation. Le plan de glissement reste le même, normal à Y=[101], et finalement nous devons avoir Z=[121]. En conséquence, le fichier contenant les constantes élastiques doit être changé pour y faire figurer la bonne orientation :

Deuxièmement, la ligne de commande elle-même doit être modifiée pour tenir compte de ces changements. Les paramètres du mode "--create" doivent être modifiés pour obtenir la bonne orientation. De plus, l'option "-dislocation" doit être modifiée pour changer le caractère de la dislocation (remplaçons "screw" par "edge"), et l'option requiert également une valeur du coefficient de Poisson (ceci est similaire à la construction d'une dislocation coin dans le cas isotrope). Cependant, puisque nous avons fourni le tenseur élastique complet, Atomsk n'utilisera pas cette valeur du coefficient de Poisson, nous pouvons donc lui donner n'importe quelle valeur (ici nous mettons simplement zéro). Au final, la ligne de commande ressemble à cela :

atomsk --create bcc 2.856 Fe orient [1-11] [-101] [121] \
-duplicate 20 30 1 \
-prop elastic.txt \
-disloc 0.501*box 0.501*box edge z y 2.47336855321 0.0 \
Fe_edge.cfg

Cette fois, le système final ressemblera à l'image ci-dessous, où les atomes sont colorés suivant les valeurs théoriques de σ_xx, aussi calculées par Atomsk en utilisant l'élasticité anisotrope :

5. Introduire une dislocation mixte

Lorsque l'élasticité anisotrope est utilisée (c'est-à-dire, quand un tenseur des constantes élastiques est fourni), il devient aussi possible de construire des dislocations mixtes. Là encore, en supposant que nous voulions que la ligne de dislocation soit suivant Z, nous devons changer l'orientation du cristal. Le plan de glissement reste normal à Y=[101]. Pour donner un exemple simple, nous choisissons X=[010] et Z=[101], de sorte que le vecteur de Burgers est simplement :

b = ½[010] + ½[101] = ½[111]

Pour construire ce système, le fichier "elastic.txt" doit être modifié comme suit :

La ligne de commande doit aussi être modifiée pour prendre en compte cete nouvelle orientation cristalline. L'option "-dislocation" doit cette fois contenir le mot-clé "mixed" (au lieu de "screw" ou "edge" précédemment), et les trois composantes cartésiennes du vecteur de Burgers, b_x, b_y, b_z, doivent être données en angströms. Ici les composantes doivent être b_x=a₀/2 et b_z=a₀/√2 (le vecteur de Burgers est contenu dans le plan de glissement normal à Y, et donc b_y=0). La ligne de commande devient alors :

atomsk --create bcc 2.856 Fe orient [0-10] [-101] [101] \
-duplicate 20 30 1 \
-prop elastic.txt \
-disloc 0.501*box 0.501*box mixed z y 1.428 0.0 2.019496967 \
Fe_mixed.cfg

En ouvrant le fichier ainsi produit "Fe_mixed.cfg" dans OVITO et en activant l'algorithme d'analyse de dislocations (en anglais dislocation analysis algorithm ou DXA), nous pouvons vérifier que la dislocation est effectivement du type ½⟨111⟩, et que le vecteur de Burgers est incliné par rapport à la ligne de dislcoation, comme on s'y attendait pour une dislocation mixte :

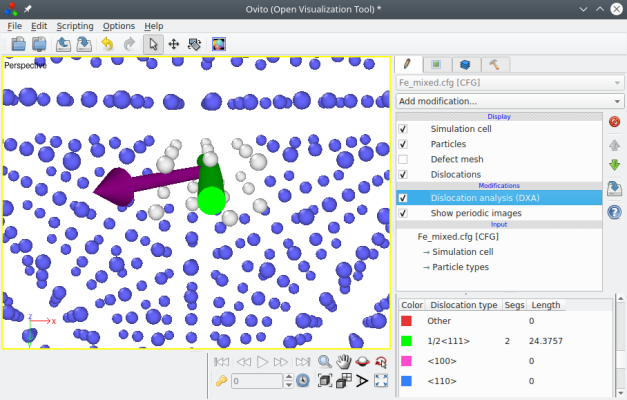
Il est ainsi possible de former des dislocations mixtes où le vecteur de Burgers forme n'importe quel angle avec la ligne de dislocation. Vous pouvez vous essayer à d'autres orientations à titre d'exercice.

6. Dernières remarques

Tout comme dans le cas isotrope, gardez en tête que les dislocations ainsi construites ne sont pas relaxées. Les contraintes théoriques calculées par Atomsk ne sont pas les "véritables" contraintes associées à la dislocation. Le but ici est de construire des dislocations qui soient proches de l'état d'équilibre, en vue d'effectuer des simulation à l'échelle atomique (avec des méthodes ab initio oou un potentiel inter-atomique).

Les configurations construites ci-dessus ne sont pas compatibles avec des conditions aux limites périodiques. Introduire une seule dislocation provoque le déplacement de tous les atomes, de sorte que les bords opposés de la boîte ne se correspondent plus. Après avoir introduit une dislocation, le système n'est plus périodique que le long de la ligne de dislocation.

Copyright © Pierre Hirel 2010-2024

Ce site Web est hébergé par l'Université de Lille