Atomsk
Le couteau suisse pour les simulations atomiques

Le couteau suisse pour les simulations atomiques

Ce tutoriel illustre trois méthodes pour construire une dislocation coin ½[110] dans l'aluminium. Il est recommandé d'être familier avec la théorie des dislocations pour suivre ce tutoriel.
▶ Pour plus d'information, référez-vous à la page de documentation correspondante.
L'aluminium est un métal cubique à faces centrées (cfc), dans lequel les systèmes de glissement sont de type ½⟨110⟩{111}. Supposons que nous voulions construire un système ne contenant qu'une seule dislocation coin, alignée avec l'axe cartésien Z, de vecteur de Burgers b=½[110], dans un plan {111} normal à Y, comme le montre le schéma ci-dessous :
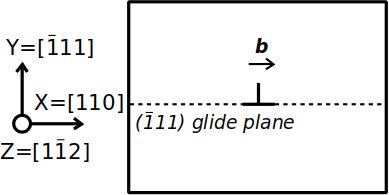
Avant toute chose, il nous faut construire une maille du cristal avec la bonne orientation qui nous permettra plus tard d'introduire la dislocation. Utilisons Atomsk pour créer une maille d'aluminium avec l'orientation X=[110] (la direction du vecteur de Burgers b), Y=[111] (normale au plan de glissement), Z=[112] :
atomsk --create fcc 4.046 Al orient [110] [-111] [1-12] Al_unitcell.xsf
ⓘ Ce paramètre de maille est donné comme exemple, et doit être ajusté selon le type de simulation que vous voulez réaliser (DFT, potentiel inter-atomique, etc.).
La visualisation par exemple avec VESTA montre à quoi ressemble cette maille :
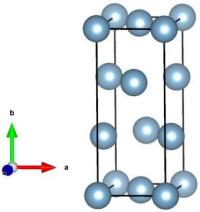
Pour pouvoir insérer une dislocation, il nous faudra un système plus grand, ou super-cellule. La dislocation est périodique suivant sa propre ligne (c'est-à-dire suivant Z), donc nous ne dupliquerons pas le système suivant cette direction. Autremen dit, le système sera "pseudo 2-D", et nous le dupliquons uniquement suivant X et Y :
atomsk Al_unitcell.xsf -duplicate 60 20 1 Al_supercell.xsf
Avec le paramètre de maille choisi ci-dessus, le vecteur de Burgers ½[110] a une magnitude |b|=a/√2=2.860954 Å. Bien entendu, si vous travaillez avec un paramètre de maille différent, alors vous devrez calculer la norme du vecteur de Burgers correspondant.
ⓘ La valeur du vecteur de Burgers doit être donné précisément, et doit être cohérent avec le paramètre de maille que vous avez choisi. Atomsk ne va pas ajuster "auto-magiquement" sa valeur.
Maintenant, il existe quatre différentes façons d'introduire une dislocation coin avec Atomsk :
Ces méthodes sont expliquées ci-dessous. Chacune d'elles a ses avantages et ses inconvénients. Aucune méthode n'est "universellement bonne", tout dépend de ce que vous souhaitez accomplir.
Une première méthode implémentée dans Atomsk consiste à appliquer les déplacements dûs à la dislocation, tout en maintenant le nombre d'atomes constant. Ceci se fait en appelant l'option "-dislocation" siovie de la position de la dislocation dans le plan XY (ici nous la placerons au milieu de la boîte), le mot-clé "edge", la direction de la ligne (Z), la normale au plan de glissement (Y), la norme du vecteur de Burgers, et le coefficient de Poisson du matériau (pour l'aluminium nous utiliserons ν=0.33) :
atomsk Al_supercell.xsf -dislocation 0.51*box 0.51*box edge Z Y 2.860954 0.33 Al_edge.cfg
ⓘ La position de la dislocation peut être entrée comme une fraction des vecteurs de boîte comme ci-dessus ("0.51*box"), ou bien directement en Angströms. La position donnée ne devrait pas correspondre exactement à la position d'un atome, sinon cet atome aurait un déplacement infini. Si vous obtenez des résultats étranges comme des discontinuités, des trous ou de larges déplacements, essayez de changer légèrement la position de la dislocation.
Dans ce cas, la partie supérieure du système est compressée, ce qui introduit une marche sur le bord à droite de la boîte, comme on peut le voir avec OVITO (voir la flèche sur l'image ci-dessous). Atomsk calcule également les contraintes théoriques (d'après la théorie de l'élasticité). Si vous souhaitez les enregistrer, alors assurez-vous que le fichier de sortie supporte les propriétés auxiliaires, comme le format CFG utilisé ici sinon ces propriétés auxiliaires sont perdues. L'image ci-dessous montre la composante σxx des contraintes, illustrant la zone de compression au-dessus du plan de glissement (en bleu) et la zone de tension en-dessous (en rouge) :
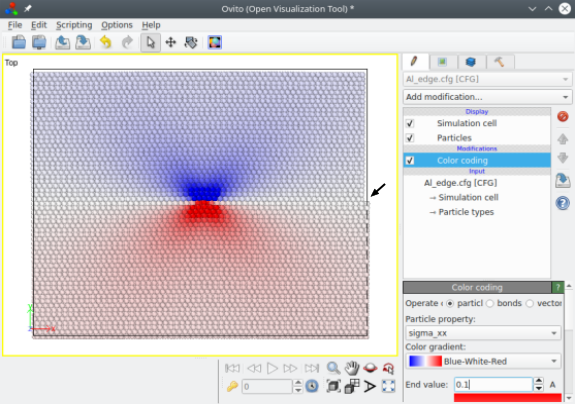
Avec cette commande, la périodicité du cristal est brisée suivant les directions X et Y, ce qui a deux conséquences. Premièrement, réaliser une simulation (relaxation, dynamique moléculaire...) sur un tel système nécessitera de figer les bords, sinon des effets indésirables et des défauts bizarres apparaîtront en bord de boîte. Deuxièmement, si vous souhaitez faire bouger cette dislocation, alors elle interagira avec ces bords figés, ce qui peut avoir un effet sur la barrière de Peierls, voire empêcher sa migration.
Une autre possibilité est d'écarter les plans atomiques au dessus du plan de glissement, et d'y insérer un nouveau demi-plan d'atomes. Avec Atomsk cela peut être fait avec la même commande que précédemment, en remplaçant simplement le mot-clé "edge" par "edge_add" :
atomsk Al_supercell.xsf -dislocation 0.51*box 0.51*box edge_add Z Y 2.860954 0.33 Al_edge_add.cfg
Cette fois, il n'y a pas de marche en bord de boîte. Toutefois, puisque de nouveaux atomes ont été introduits, le système s'est agrandi suivant l'axe X. Si des conditions au limites étaient appliquées, alors certains atomes risqueraient de se chevaucher. Pour empêcher cela, Atomsk allonge la boîte suivant X d'une quantité b/2.
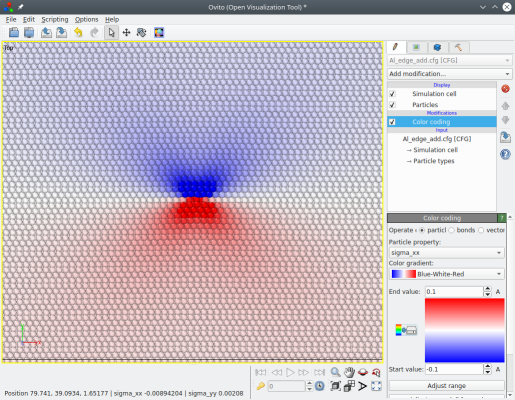
Comme précédemment, la périodicité du système est perdue suivant X et Y. Une autre conséquence est que de nouveaux atomes ont été introduits (à la fin de la liste d'atomes), ce qui rend plus difficile la comparaison de ce système avec la super-cellule de référence que nous avions au départ ("Al_supercell.xsf").
Une autre possibilité est de supprimer un demi-plan d'atomes en-dessous du plan de glissement, puis de resserrer les plans atomiques dans la moitié basse du cristal. Dans la commande ci-dessus, utilisez cette fois le mot-clé "edge_rm" :
atomsk Al_supercell.xsf -dislocation 0.51*box 0.51*box edge_rm Z Y 2.860954 0.33 Al_edge_rm.cfg
Comme dans la méthode précédente, aucune marche n'est formée sur les bords. Cependant, comme des atomes ont été supprimés, le système s'est raccourci suivant X. Pour en tenir compte, Atomsk raccourcit la boîte suivant X d'une quantité b/2.
Les méthodes précédentes ont toutes le même inconvénient : le système final n'est plus périodique suivant la direction du glissement (ici suivant X), elles ne sont donc pas adaptées pour étudier le glissement d'une dislocation seule. Afin de construire un système périodique, une autre méthode existe : superposer deux cristaux, celui du dessus contenant une colonne d'atomes en plus par rapport au cristal inférieur. Pour faire coïncider leurs longueurs, le cristal du haut est comprimé de b/2, et celui du bas allongé de b/2.
Commençons par construire ces deux blocs. Le cristal du baas contient N=40 colonnes atomiques, et est allongé d'une demi-maille suivant X, c'est-à-dire de 0.5/40=0.0125 :
atomsk Al_unitcell.xsf -duplicate 40 10 1 -deform X 0.0125 0.0 bottom.xsf
Ici nous utilisons l'option "-deform" avec un coefficient de Poisson nul, autrement dit il s'agit d'une déformation uniaxiale pure. De façon similaire, le cristal du haut est construit avec N+1=41 colonnes atomiques, et comprimé suivant X de 0.5/41=0.012195122 :
atomsk Al_unitcell.xsf -duplicate 41 10 1 -deform X -0.012195122 0.0 top.xsf
Ensuite, le mode "--merge" peut être utilisé pour superposer les deux cristaux suivant Y :
atomsk --merge Y 2 bottom.xsf top.xsf Al_edge_bicrystal.cfg
Le système final ("Al_edge_bicrystal.cfg") ne contient pas encore de dislocation. Il contient seulement deux cristaux qui ont un désaccord de réseau croissant suivant X, comme on peut le voir dans OVITO (ici les atomes sont colorés suivant leur critère de centro-symétrie) :
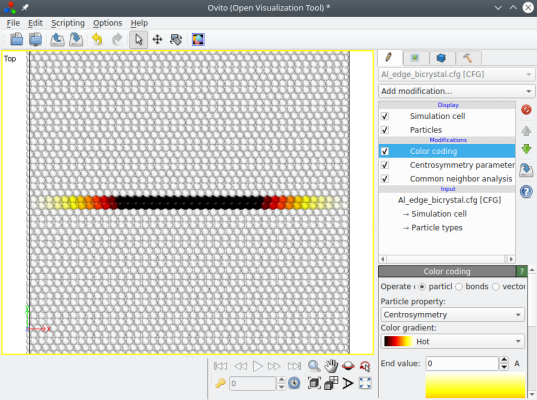
Ce système est loin de l'équilibre, et c'est seulement après une simulation qu'il relaxera pour former une dislocation coin. L'avantage de cette méthode est que le système est périodique suivant la direction X, ce qui rend possible l'application d'une contrainte de cisaillement pour observer le mouvement de la dislocation. Cependant, ce système n'est toujours pas périodique suivant Y, et il peut être nécessaire de figer les atomes proches des bords supérieur et inférieur.
Il est possible d'introduire plusieurs dislocations coin dans le système. Pour cela, appelez l'option "-dislocation" plusieurs fois, en modifiant la position et le vecteur de Burgers selon vos besoins.
Par exemple, la commande suivante introduit deux dislocations coin de vecteurs de Burgers opposés, la première aux coordonnées réduites (¼ ¼), et la seconde en (¾ ¾) :
atomsk Al_supercell.xsf -dislocation 0.251*box 0.251*box edge_add Z Y 2.860954 0.33 \
-dislocation 0.75*box 0.751*box edge_add Z Y -2.860954 0.33 Al_edge_dipole.cfg
Quand plusieurs dislocations sont insérées, leurs contributions aux contraintes s'ajoutent, comme on peut le visualiser :
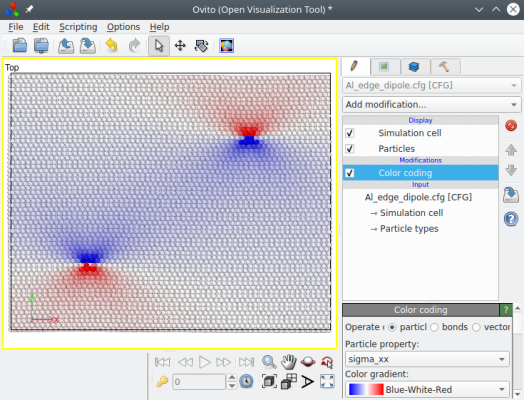
L'avantage d'un tel dipôle (ou d'un quadripôle) est que la somme des vecteurs de Burgers est un vecteur nul, et donc à longue portée la somme de leurs déplacements élastiques tend à s'annuler. Résultat, aucun artefact ne devrait apparaître aux bords de boîte, et le système est périodique dans les trois dimensions.
Les dislocations construites avec les méthodes ci-dessus ne sont pas relaxées ni optimisées. Elles correspondent, au mieux, aux champs de déplacements prédits par la théorie élastique des dislocations. Toutefois, afin d'obtenir la véritable configuration atomique des dislocations, il sera nécessaire de réaliser une simulation avec une méthode ab initio ou un potentiel inter-atomique. Par exemple, dans le cas de l'aluminium, on s'attend à ce qu'une dislocation ½[110] se dissocie en deux dislocations partielles de Shockley. En fonction de la méthode choisie ci-dessus, la dislocation peut interagir avec des bords figés, l'empêchant de se dissocier pleinement et introduisant des effets indésirables. Vous aurez peut-être à tester différentes tailles de boîtes, et différentes méthodes, avant d'être sûr que vos résultats soient cohérents.
Ce tutoriel s'est focalisé sur les dislocations à caractère purement coin, il est aussi possible de construire des dislocations à caractère vis comme le montre le tutoriel suivant.
Par défaut, l'option "-dislocation" applique les champs de déplacement de l'élasticité isotrope. Cela se justifie dans le cas de l'aluminium, qui est un matériau relativement isotrope. Dans les matériaux où l'anisotropie est très prononcée, il peut être préférable d'utiliser les équations de l'élasticité anisotrope, comme expliqué dans ce tutoriel.