Atomsk
Le couteau suisse pour les simulations atomiques

Le couteau suisse pour les simulations atomiques

Ce tutoriel illustre comment utiliser Atomsk pour construire un système contenant une dislocation et une inclusion sphérique, en prenant comme exemple une sphère de silicium dans une matrice d'aluminium.
Commençons par construire la matrice d'aluminium cfc. Pour des raisons de simplicité, nous allons introduire le même type de dislocation vis que dans un tutoriel précédent -référez-vous à ce tutoriel pour en savoir plus sur ce type de dislocation.
Contrairement au tutoriel précédent où le système ne contenait qu'une dislocation, ici nous voulons que le système soit suffisamment large pour contenir aussi une inclusion sphérique. Autrement dit, le système doit être assez large dans les trois dimensions de l'espace. Nous plaçons la dislocation en (X=0,25;Y=0,5), et la sphère en (X=0,75;Y=0,5) avec un rayon de 20 Å.
Tout cela peut être réalisé avec une seule commande :
atomsk --create fcc 4.046 Al orient [1-12] [-111] [110] \
-duplicate 50 30 30 \
-dislocation 0.251*box 0.501*box screw Z Y 2.860954 \
-select in sphere 0.75*box 0.5*box 0.5*box 20 \
-remove-atoms select \
fccAl_matrix.cfg
Voici ce que signifie cette commande : une maille élémentaire d'aluminium cfc est créée (grâce au mode "--create"), puis elle est dupliquée dans les trois directions de l'espace pour former une super-cellule de 50×30×30. Ensuite, la dislocation est insérée (voir tutoriel précédent), et enfin, une sphère d'atomes est sélectionnée, puis supprimée.
Le système final ("fccAl_matrix.cfg") est relativement large, il contient environ 270 000 atomes. Il peut être visualisé avec Atomeye :
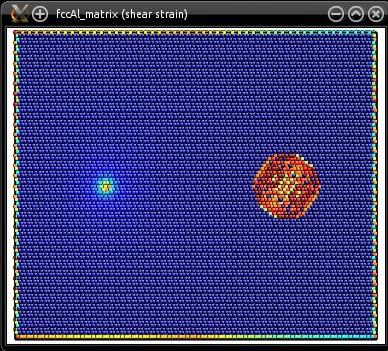
Comme expliqué dans le tutoriel précédent, puisque nous avons inséré une seule dislocation, les conditions aux limites ne peuvent plus être périodiques dans les conditions X et Y.
Pour l'instant, nous avons un système d'aluminium qui contient juste un trou sphérique. Maintenant, attelons-nous à la construction de la sphère de silicium. Cette sphère doit être placée exactement à la même position que le trou que nous avons creusé dans l'aluminium. Atomsk doit avoir affiché à l'écran la position de la sphère en Å lorsque vous avez exécuté la commande précédente : il a dû afficher "(185.824,105.118,42.914)". Cette position peut aussi être calculée "manuellement", par exemple suivant X la maille de départ a un vecteur 1/2[112], de longueur 4.046*√6/2=9,91063 Å, et nous l'avons dupliquée 50 fois suivant X, donnant une longueur totale de boîte de 247,7658 Å. La sphère est placée à 0,75 fois cette longueur, c'est à dire X=185,824 Å, ce qui est bien la valeur affichée par Atomsk. De façon similaire, la position de la sphère peut être calculée suivant Y et Z.
La façon la plus simple de construire une sphère de silicium exactement à cet endroit, est de construire une super-cellule de silicium extrêmement grande (au moins aussi grande que le système de silicium), et ensuite d'y tailler la sphère. Remarquez que cette fois, nous devons sélectionner les atomes à l'extérieur de la sphère pour les supprimer :
atomsk --create diamond 5.431 Si \
-duplicate 60 40 40 \
-select out sphere 185.824 105.118 42.914 20 \
-remove-atoms select \
Si_sphere.cfg
La visualisation montre que la sphère semble être au bon endroit :
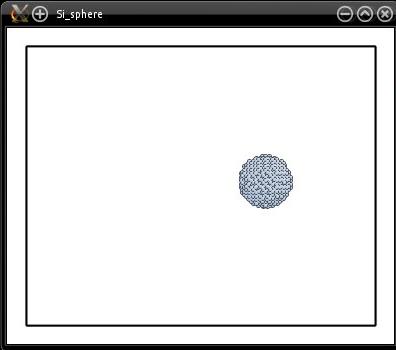
L'inconvénient de cette méthode est que nous générons une très grande boîte de silicium contenant beaucoup d'atomes, pour ensuite en supprimer la plus grande partie et n'en conserver qu'une petite sphère de 20 Å de rayon. Cela utilise beaucoup de mémoire et de temps de calcul pour pas grand chose. Une solution alternative, moins gourmande, est de construire un système plus petit, juste un peu plus grand que la sphère, puis d'y creuser la sphère, et enfin de la déplacer au bon endroit avec l'option "-shift" :
atomsk --create diamond 5.431 Si \
-duplicate 10 10 10 \
-shift -0.5*box -0.5*box -0.5*box \
-select out sphere 0 0 0 20 \
-remove-atoms select \
-select none \
-shift 185.824 105.118 42.914 \
Si_sphere.cfg xsf
Cette commande est résumée par le schéma suivant :
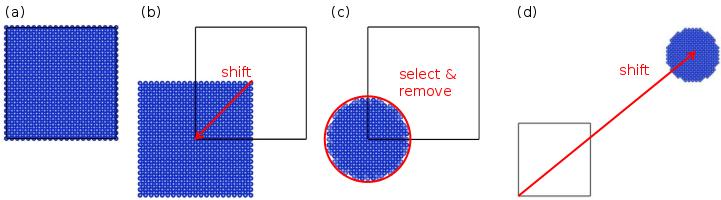
(a) Une maille élémentaire de silicium est créée et dupliquée pour former une super-cellule. La boîte est représentée par des lignes noires.
(b) Tous les atomes sont translatés de (-0,5;-0,5;-0,5) en coordonnées réduites. Notez que du coup, certains atomes se retrouvent en dehors de la boîte.
(c) Une sphère de rayon 20 Å est sélectionnée, centrée sur l'origine (0,0,0). Les atomes en-dehors de cette sphère sont supprimés.
(d) Les atomes restants sont translatés jusqu'à la position voulue (dans ce schéma les distances ne sont pas respectées).
Si vous essayez de visualiser le système final, certains logiciels de visualisation (comme Atomeye ou VESTA) montreront les atomes comme s'ils étaient dans la boîte. C'est parce que ces logiciels appliquent automatiquement des conditions aux limites périodiques, et replacent les atomes dans la boîte. Cependant si vous visualisez le système avec OVITO, vous verrez bien la sphère d'atomes en dehors de la boîte, aux coordonnées cartésiennes que nous avons indiquées.
Maintenant, il ne nous reste plus qu'à réunir les deux systèmes dans la même boîte :
atomsk --merge 2 fccAl_matrix.cfg Si_sphere.cfg AlSi_final.cfg
Le nombre "2" indique que deux systèmes doivent être réunis (dont les noms apparaissent ensuite). Lorsque plusieurs systèmes sont réunis dans la même boîte, alors la boîte finale a exactement les dimensions de la boîte du premier système. Ici, nous devons donc fournir la matrice d'aluminium en premier, car c'est elle qui sera la boîte finale. Les atomes de silicium sont simplement ajoutés dans cette boîte (la boîte du système de silicium n'est pas utilisée, et est simplement perdue). Ainsi, vous pouvez utiliser l'une ou l'autre méthode ci-dessus pour construire la sphère de silicium, cela n'aura aucun impact sur le résultat final -la seule chose qui compte, c'est que la sphère de silicium soit aux bonnes coordonnées cartésiennes.
Le résultat final est écrit dans le fichier "AlSi_final.cfg", et sa visualisation montre bien la ligne de dislocation dans l'aluminium et l'inclusion de silicium (les atomes dans un environnement parfait ne sont pas affichés afin de faciliter la visualisation) :

Comme dans un précédent tutoriel, la dislocation vis que nous avons insérée n'est pas relaxée. Il est aussi possible de restaurer la périodicité suivant X, en modifiant les vecteurs de la boîte finale. Cela peut être utile avant d'appliquer une contrainte pour faire bouger la dislocation, et la voir interagir avec l'inclusion.
Nous n'avons pas spécifié d'orientation cristallographique particulière pour la sphère de silicium -elle est juste orientée X=[100], Y=[010], Z=[001]. Bien sûr, au moment de sa création, il est possible de lui donner une autre orientation. Il est aussi possible de choisir un autre rayon, ou une autre forme, par exemple un cube, un parallélépipède, ou encore un cylindre.