Atomsk - Tutoriel - Boucle de Dislocation Prismatique

Tutoriel : Boucle de Dislocation Prismatique

Ce tutoriel explique comment construire une boucle de dislocation partielle de Frank ⅓[111], un type de boucle prismatique, dans l'aluminium. Il est recommandé d'être familier avec la théorie des dislocations afin de suivre ce tutoriel.

▶ Pour plus d'information, référez-vous à la page de documentation correspondante.

ⓘ Ce tutoriel porte sur les boucles prismatiques, ou boucles de montée, où le vecteur de Burgers est normal au plan de la boucle. Pour les boucles glissiles, suivez plutôt ce tutoriel.

1. Orientation cristallographique du système

Comme dans les tutoriels précédents, la première étape est de construire une super-cellule avec l'orientation cristallographique appropriée. De plus, elle doit être assez large suivant les trois directions de l'espace pour pouvoir insérer une boucle :

atomsk --create fcc 4.046 Al orient [11-2] [111] [-110] -duplicate 20 14 30 Al_supercell.xsf

Nous souhaitons introduire une boucle de dislocation partielle de Frank, de vecteur de Burgers b=⅓[111], dans le plan (111). Avec l'orientation que nous avons choisie, les coordonnées cartésiennes du vecteur de Burgers seront b = (0 b_y 0), où b_y = a₀×√3/3 ≈ 2.336 Å.

ⓘ Pour ce type de boucle de dislocation, le vecteur de Burgers b est normal au plan de la boucle. Dans notre exemple, le plan de la boucle est normal à Y, donc b est aussi suivant Y.

2. Supprimer un disque d'atomes

Comme première approche naïve, une partielle de Frank peut être obtenue en supprimant un disque d'atomes dans le plan (111). Dans Atomsk, cela peut être réalisé en combinant plusieurs sélections. D'abord, sélectionnons tous les atomes appartenant à un cylindre du rayon voulu, dont l'axe principal est normal au plan (111), donc suivant Y. Puis, retirons de cette sélection les atomes situés en-dessous d'une certaine coordonnée y_min, ainsi que les atomes au-dessus de y_max. Il faut s'assurer que y_max−y_min est égal à la norme du vecteur de Burgers b_y, de sorte qu'un seul plan (111) soit sélectionné. Dans l'exemple ci-dessous, nous utilisons y_min = 50 Å et y_max = 52.336 Å. Enfin, une fois que cette sélection est bien définie, supprimons les atomes ainsi sélectionnés :

atomsk Al_supercell.xsf \
-select in cylinder Y 0.5*box 0.5*box 20 \
-select rm below 50.0 Y \
-select rm above 52.336 Y \
-remove-atoms select \
loop1.cfg

ⓘ L'option "-select" est utilisée ici pour sélectionner et dé-sélectionner des atomes. Cette option ne supprime aucun atome elle-même, elle ne fait qu'ajouter ou retirer des atomes à la sélection. Seule l'option "-rmatoms" supprime véritablement des atomes. Pour en savoir plus, lisez ce tutoriel.

Vous pouvez ensuite ouvrir le fichier CFG final avec OVITO. Dans la figure ci-dessous, les atomes sont colorés en fonction de la critère de centro-symétrie (les atomes en blanc sont dans un environnement cfc parfait, les atomes colorés ne le sont pas), et les atomes de coordonnée Z inférieure à la moitié de la boîte ont été supprimés pour faciliter la visualisation (le système a été "coupé en deux" suivant Z dans OVITO). Nous pouvons voir que supprimer un disque d'atomes crée un vide dans le matériau, ce qui n'est pas très réaliste, mais peut servir de point de départ pour une simulation.

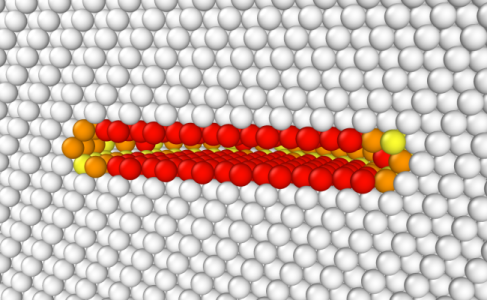
3. Utiliser l'option "-dislocation loop"

Au lieu de supprimer "manuellement" un disque d'atomes, il est possible d'utiliser l'option "-dislocation loop" de Atomsk. Plaçons la boucle au centre de la boîte (0.5*box along each direction), normale à l'axe Y, et choisissons un rayon de 14 Å pour la boucle. Contrairement au tutoriel précédent, cette fois nous donnons au vecteur de Burgers une composante uniquement suivant Y, autrement dit le vecteur de Burgers est b = (0 b_y 0). Enfin, nous utilisons un coefficient de Poisson de 0.33, une valeur typique de l'aluminium :

atomsk Al_supercell.xsf \
-dislocation loop 0.5*box 0.5*box 0.5*box Y 14 0 -2.336 0 0.33 \
loop2.cfg

ⓘ Une valeur négative de la composante du vecteur de Burgers signifie que des atomes sont supprimés. Ce type de boucle est parfois appelée boucle de Frank négative, boucle lacunaire, défaut d'empilement intrinsèque, ou partielle de Frank de type S (le "S" signifie qu'il y a un Seul défaut d'empilement).

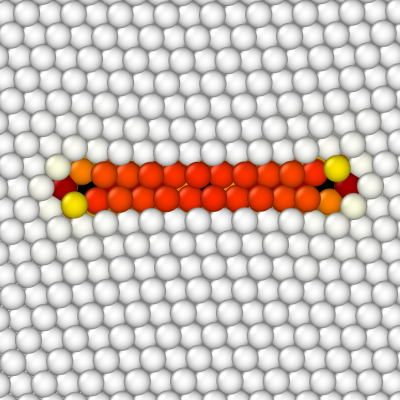
Atomsk supprime les atomes à l'intérieur de la boucle, et ensuite applique les déplacements due à la dislocation à tous les atomes. Donc, contrairement à la section précédente (où nous avions supprimé un disque), cette fois il n'y a pas de vide dans le matériau.

Nous pouvons ouvrir le ficher CFG final avec OVITO, et colorer les atomes selon le critère de centro-symétrie. En plus, l'algorithme d'analyse de dislocations (en anglais dislocation analysis algorithm ou DXA) est utilisé pour obtenir un contour de la ligne de dislocation (assurez-vous de choisir le réseau CFC). Cet algorithme trouve bien une partielle de Frank (ligne en cyan), comme nous le voulions.

4. Partielle de Frank positive

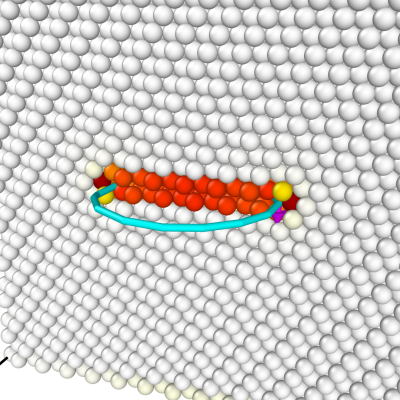
Avec la même commande, en changeant uniquement le signe de la composante b_y du vecteur de Burgers, nous pouvons construire une boucle de Frank positive :

atomsk Al_supercell.xsf \
-dislocation loop 0.5*box 0.5*box 0.5*box Y 14 0 2.336 0 0.33 \
loop3.cfg

ⓘ Une valeur positive de la composante du vecteur de Burgers signifie qu'un nouveau plan d'atomes est introduit dans le système. Ce type de boucle est parfois appelé boucle de Frank positive, boucle interstitielle, défaut d'empilement extrinsèque, ou partielle de Frank de type D (le "D" signifie qu'il y a un Double défaut d'empilement).

Cette fois, les atomes à l'intérieur de la boucle sont dupliqués, puis les déplacements élastiques sont appliqués à tous les autres atomes.

7. Dernières remarques

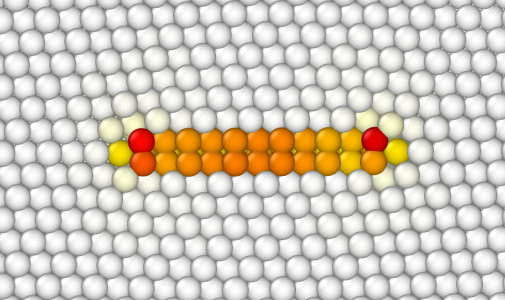
Comme dans les tutoriels précédents, lors de la construction de boucles de dislocations, l'utilisateur doit bien réfléchir à la géométrie de son système, au vecteur de Burgers, au plan, et à la position de la boucle. N'hésitez pas à essayer différentes tailles de boîte, différentes positions, et différents rayon. Si certains points de la boucle sont en-dehors de la boîte, Atomsk affichera un avertissement ; c'est à vous de décider si c'est le résultat voulu ou non. Notez que l'option "-dislocation" n'utilise pas de conditions aux limites périodiques, donc si certains points d'une boucle sont en-dehors de la boîte, ils ne seront pas remis automatiquement de l'autre côté de la boîte&nbps;: ils seront simplement complètement en dehors du système atomique, comme s'il y avait une surface libre.

Enfin, comme pour les dislocations rectilignes, la boucle de dislocation introduite ici n'est pas relaxée ni optimisée, mais elle peut être utile comme point de départ pour une simulation. Les partielles de Frank sont connues pour être sessiles, cependant selon les conditions de la simulation elles peuvent se dissocier en d'autres types de dislocations. Si vous n'êtes pas sûr de la façon de procéder, veuillez vous référer à un livre sur les dislocations.